So saßen wir also da bei einem unserer Spielenachmittage Anfang 2019 und kamen nach einer Runde Pandamie auf unsere Studentenzeiten. Lange ist es her. Ende der Achtziger trafen wir uns nicht nur zu Brettspielen wie Titan, 1830 und Civilization, sondern auch zu dem wohl ersten netzwerkfähigen Spiel überhaupt. MidiMaze – erschienen 1987 für den Atari ST. Bis zu 16 Computer konnten über die Midi-Schnitttstelle, die eigentlich für den Anschluss von Keyborads und Synthesizern konzipiert wurde, in einem Ring verbunden werden. Ich kann mich noch gut daran erinnern, wie in meiner Studentenbude 13 Mädchen und Jungs gezockt haben.

Dabei war es nicht so wie heute, dass jeder sein Notebook mitgebracht hat und über WLAN kurzerhand die Verbindung hergestellt wurde. Damals hieß es den Rechner, den Röhrenmonitor, das Diskettenlaufwerk samt diverser Brickets – so nannten wir die einzelnen Netzteile für die Komponenten – zum Zielort zu schleppen, mit den Midikabeln zu verbinden und darauf zu hoffen, dass der Ring auch funktionierte. So saßen wir also da, auf dem Boden, verteilt auf alle Räume – unsere WG hatte ganze 48 m² auf drei Zimmer, Küche, Flur und Bad verteilt -, dazwischen die Hardware und jede Menge Kabel. Und wehe, jemand blieb beim Gang auf die Toilette an einem Kabel hängen und hat den Ring getrennt…
Na, jedenfalls hatten wir damals eine Menge Spaß. Und so kam es, dass ich letztes Jahr nach einer Version für Windows gesucht habe. Aber bis auf WinMaze, das 1994 von Nils Schneider geschrieben wurde, habe ich nichts gefunden. Nach vielen Versuchen und Installation diverser Komponenten, habe ich das Spiel auch unter Windows 7 und Windows 10 zum Laufen gebracht, aber leider scheiterte das Ganze an der Netzwerkverbindung. Sobald sich ein dritter Spieler eingeloggt hat, wurde der vorherige Spieler rausgeschmissen. Somit konnten nur zwei Leute spielen – was auf Dauer keinen Spaß macht. Denn der Spaß steigt mit der Anzahl der Mitspieler.
Frustriert habe ich das Ganze dann aufgegeben. Aber im Hinterkopf hat sich der Gedanke festgesetzt, ein eigenes MidiMaze zu programmieren – wenn ich mal Zeit habe (the famous last words). Dann kam der Corona-Lockdown und ich hatte Zeit. Somit begann das Abenteuer PlanetMaze…
Wenn man anfängt sich mit der Materie näher zu befassen, stellt man fest: Uups, das Ganze klingt leichter, als es ist. Prinzipiell geht es darum, 3D-Objekte im Raum zu bewegen und Kollisionen zwischen den Objekten zu ermitteln. Und dann ist man mitten drin im Karthesischen Koordinatensystem, Zylinderkoordinatensystem und zuguter letzt dem Kugelkoordinatensystem sowie der Umrechnung zwischen den einzelnen Korrdinatensystemen.

Also wieder die Mathematik aus der Schul- und Studentenzeit herausgekrammt und sich mit Translationen, Rotationen und Skalierung von 3D-Objekten im Raum beschäftigt. Grundlage dafür sind Berechnungen auf Basis von vierdimensionalen Matrizen.
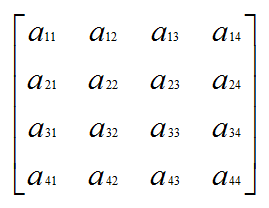
Die nächsten Stolpersteine waren die 3D-Objekte. Wie zeichnet man eine Kugel, einen Würfel oder komplexere Objekte? Es basiert alles auf Dreiecken, die im Raum entsprechend angeordnet, das gewünschte Objekt darstellen sollen. Je mehr Dreiecke verwendet werden, umso realistischer das Aussehen (z.B. eine Kugel).
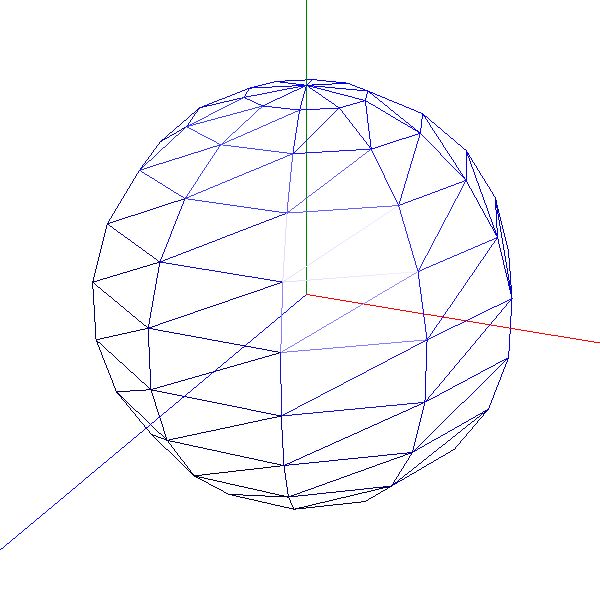
Kugelmodel mit 10 Segmenten 
Kugelmodel mit 50 Segmenten
Was fängt man aber mit einem Drahtgeflecht an? Dieses Skelett benötigt noch einen Überzug, um als Kugel wahrgenommen zu werden. Und für diese Aufgabe kommt noch ein zusätzliches viertes Koordinatensystem hinzu. Die sogenannten UV-Koordinaten legen fest, wie Teile eines zweidimensionalen Bildes auf die einzelnen Teilflächen der Gitterstruktur aufgespannt werden.
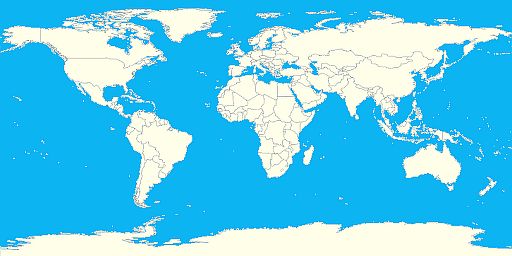
Spannt man das obige zweidimensonale Bild auf die zwei Gitterstrukturen, so erhält man mehr oder weniger eine Kugel.
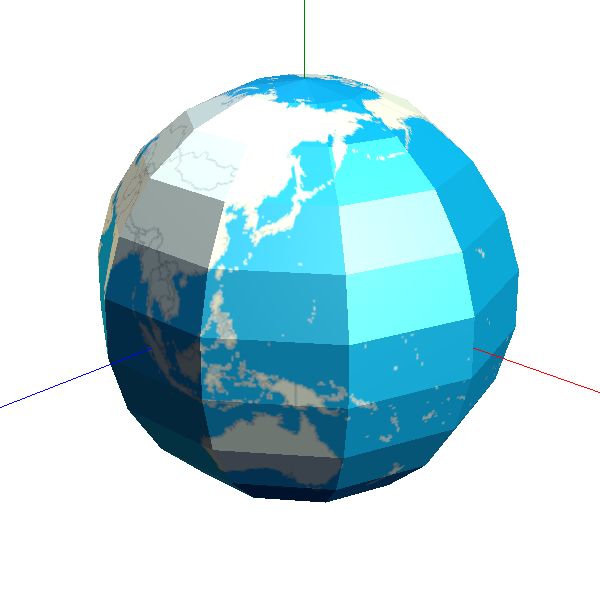
Textur auf 10-Segment Kugel 
Textur auf 50-Segment Kugel
Verwendet man ein detaillierteres Bild, so erscheint die Kugel noch realistischer.

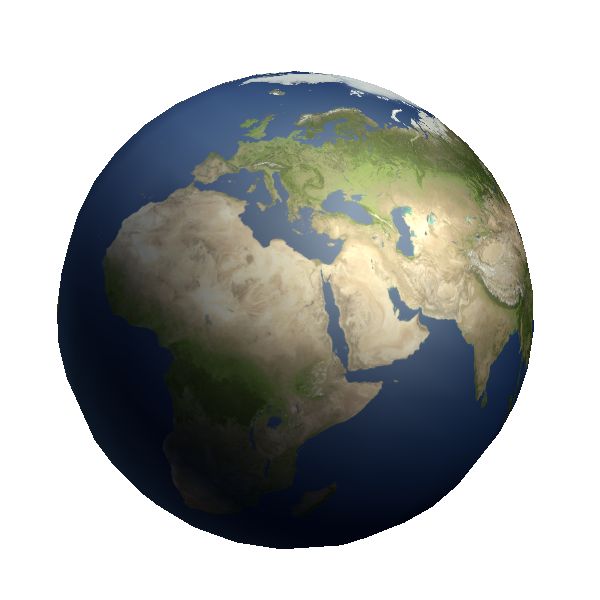
War das schon alles? Natürlich nicht! Diese Welt ist zu ideal, zu glatt. Es fehlt einfach an Tiefe. Die Art und Weise, wie so eine Textur auf dem Gitterrahmen gezeichent wird, wird durch den sogenannten Shader berechnet. Moderne Graphikkarten können direkt programmiert werden. Das geschieht mittels der HLSL (High Level Shading Language) Programmiersparache. Hierbei wird der Graphikkarte ein Programm übergeben, dass anhand der Normalenvektoren eines Objektes die Licht-, Farb- und Spiegelintensität berechnet. Dieser Vorgang wird Shading genannt. Um so ein Shading durchführen zu können, muss für die zu verwendende Textur eine sogenannte Normalen-Map erzeugt werden. Für die oben dargestellte Erde, sieht diese, wie folgt aus (wobei es verschiedene Varianten geben kann):
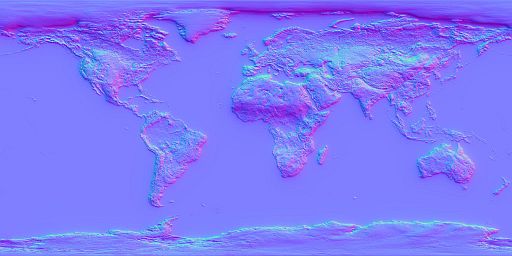

Flache Textur 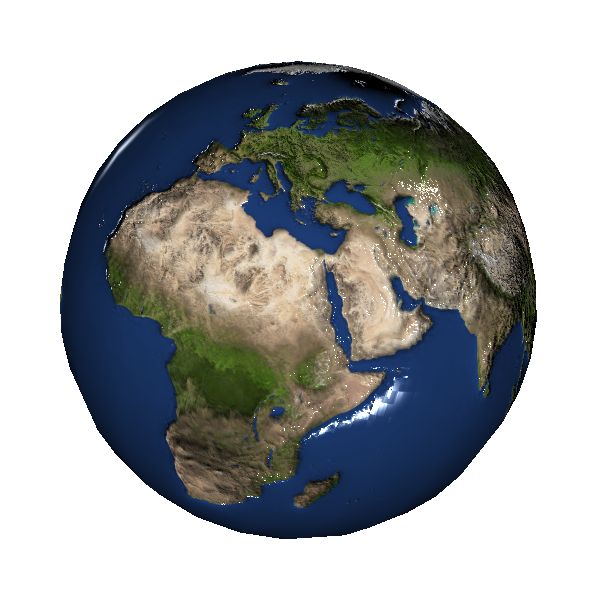
Textur mit Normalen-Map
Das Ergebnis ist dann, eine reliefartige Darstellung der Welt. Wie stark der 3D-Effekt ausfällt, hängt von der Normal-Map und dem programmierten Shader ab.
Einfache 3D-Objekte, wie Würfel, Kugeln, Tetraeder, Kegel und Objekte, die durch Rotation entstehen, können noch in der Anwendung modelliert werden. Sind Objekte aber komplexer und bestehen aus vielen Tausend Dreiecken, so greift man auf 3D-Modellierungsprogramme zurück, deren Ergebnis das gewünscht Model ist, das wiederum mit einer Textur überzogen wird und dem man mittel einer Normalen-Map und eines entsprechenden Shaders Tiefe geben kann.

Auf diesen Grundlagen entstand das erste Smiley – noch in der Anwendung programmiert -, das über einer Grundfläche mit Schachbrettmuster hüpfte. Das Smiley, obwohl eine Kugel, sah noch flach aus, aber es hüpfte bereits über die Spielfläche und mit einer über die Tastatur gesteuerten Kamera konnte man dieselbe über das Spielfeld bewegen und das Smiley aus unterschiedlichen Perspektiven betrachten. Und das Herz schlug schneller.

Wenn man glaubt, dass man jetzt alle Grundlagen zur Verfügung hat, um ein Spiel zu programmieren, wird man ganz schnell auf den Boden der Tatsachen verfrachtet – facing reality!
Erstens muss man sich jetzt mit der Kamera beschäftigen. Die wichtigsten Aspekte sind hier die Position, die Blickrichtung und der Blickwinkel der Kamera. Und jetzt kommen mehrere Bewegungen hinzu, die komplett voneinander unabhängig sind, aber das, was der Spieler sieht, bestimmen. Sowohl der/die Spieler als auch die Kamera bewegen sich im Raum und ensprechend der Blickrichtung und des Blickwinkels der Kamera muss das Bild berechnet werden. Die Kamera kann dabei aus einer Vogelperspektive auf das Geschehen im Maze blicken oder aus der Sicht eines Spielers – sich also im Smiley befinden und aus dessen Blickrichtung die Szenerie aufnehmen. Bei der Berechnung der gesamten darzustellenden Szenerie aus Smiley-Sicht kommt man dann schnell an die Grenze des Vorstellungsvermögens und sitzt dann morgens am Frühstückstisch und macht seltsame Bewegungen mit dem weichgekochten Ei (Smiley) in der einen Hand und einem Salzstreuer (Kamera) in der anderen Hand. So versucht man sich also bildlich die Abläufe zu verdeutlichen, die im Maze stattfinden. Und siehe da, es hilft. Man landet dann irgendwann bei inversen Matrizen und prompt stellen Smiley und Kamera die Szenerie so da, wie man es sich vorstellt.
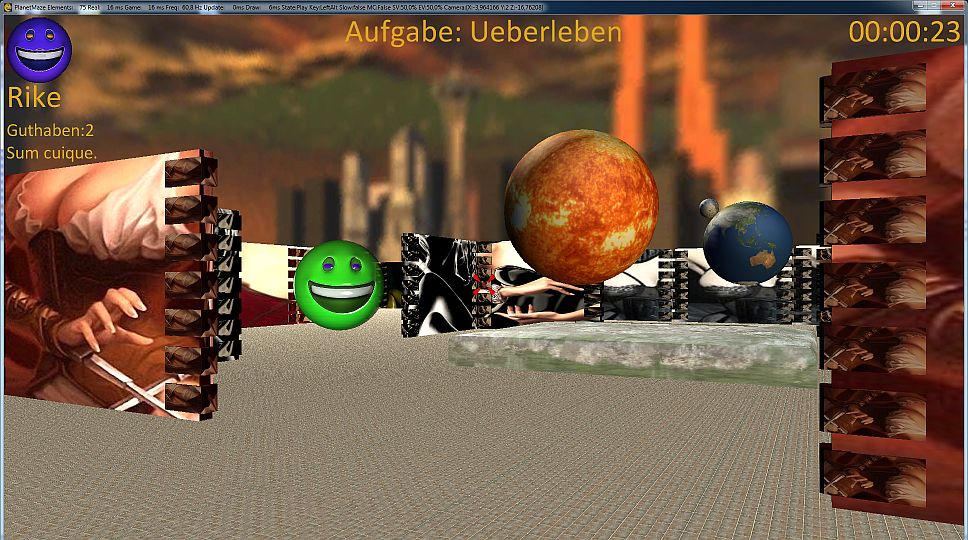
Zweitens häuften sich jetzt die Probleme. Hat man den Aufbau des Mazes aus einzelnen Objekten soweit umgesetzt, dann stellt man fest, dass die Smileys dummerweise durch die Wände rennen können – klar, woher sollen die auch wissen, dass eine Wand hart ist und ein Hindernis darstellt? Das Ganze sieht dann so aus:

Autsch, das tut weh. Somit hat man das nächste Thema und das hört auf den Namen Kollisionsermittlung. Die benötigt man nicht nur, wenn das Smiley durch das Labyrinth rennen soll – und zwar nur auf den zulässigen Pfaden, sondern auch, wenn das Smiley ein Tor öffen soll, einen Schlüssel einsammeln soll und natürlich auch wenn es durch einen Fireball getroffen wird.
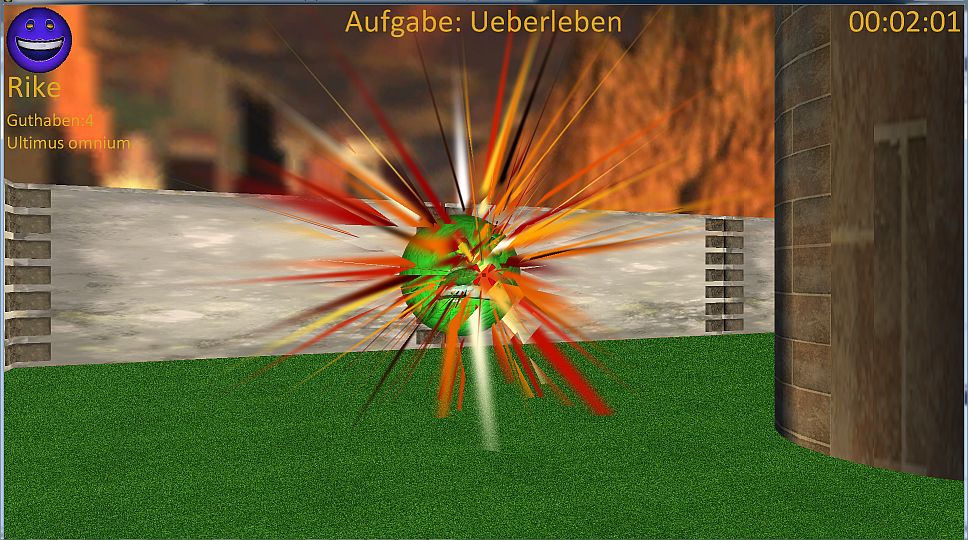
Es gibt verschiedene Arten der Kollisionsermittlung. Vereinfacht gesagt bildet man um das Objekt ein oder mehrere umfassende Körper. So kann man z.B. um eine Wand einen Quader (BoundingBox) oder eine oder mehrere Kugeln (BoundingSphere) oder auch andere Körper berechnen, die das Objekt umfassen.
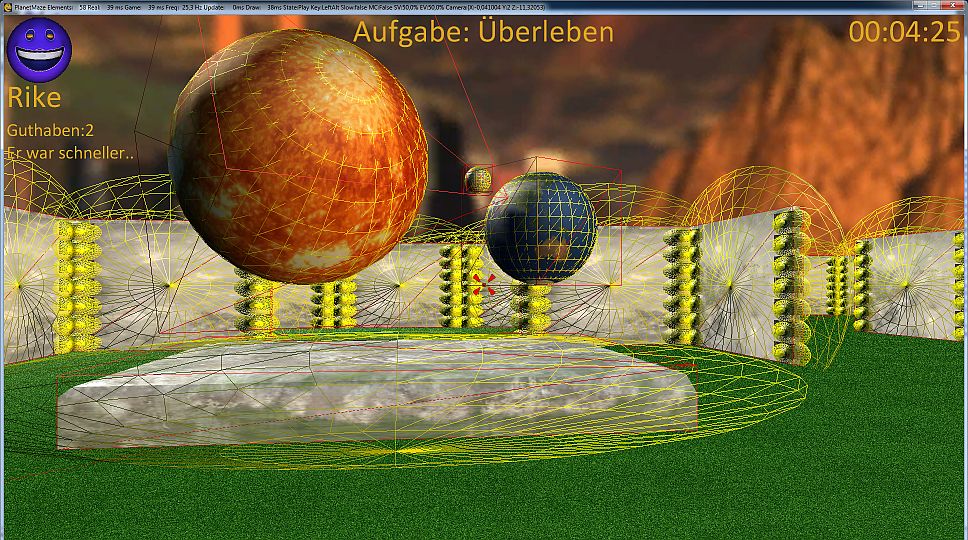
Alle haben aber gemeinsam, dass eine Kollision immer dann vorliegt, wenn sich zwei Objekte schneiden. Es gibt vereinfachte Verfahren, die vorraussetzen, dass die umgebenden Quader (bei drei Dimensionen) bzw. Rechtecke (bei zwei Dimensionen) an den Achsen ausgerichtet werden müssen – eine sogenannte AABB (Axis Aligned Bounding Boxes) Kollisionsermittlung. Eine Überschneidung kann auch zwischen unterschiedlichen umfassenden Körpern berechnet werden oder z.B. auch zwischen einem Körper und einem Strahl (Ray), der z.B. den Vektor einer Bewegung darstellt. Graphisch sieht das ganze dann so aus:

Somit alles klar? Leider wieder nicht. Die Kollisionsermittlung funktionierte zwar jetzt und die Smileys blieben an den Wänden „hängen“. Aber leider nicht immer. Es gab Situationen, in denen das Smiley aus bestimmten Winkeln bzw. Positionen durch eine Wand durchlaufen konnte, aber nicht bei der Wand daneben? Dies hatte mit der Bewegungsgeschwindigkeit zu tun. War das Smiley so schnell unterwegs, dass es zwischen zwei Positionsberechnungen den gesamten Weg von der Position vor der Wand bis zur Position hinter der Wand zurückgelegt hat, konnte es durch Wände gehen – ja das ist wahre Magie! Aber auch das ließ sich lösen, indem man den Geschwindigkeitsvektor bei de Kollisonsermittlung mitberücksichtigt.
Soviel zu den Grundlagen. Mit diesem Rüstzeug konnte das große Abenteuer PlanetMaze gestartet werden. Und wie ging es weiter? Nachdenken, Ideen, Phantasie und viel programmieren. Ich hoffe, sie haben genauso viel Spaß beim Spielen, wie ich beim Programmieren von PlanetMaze hatte.

